第5回 一目均衡表 その応用的活用法-時間論、波動論、水準論
一目均衡表には、時間論、波動論、水準論というものがあります。
時間論
時間論で基本となるのが「基本数値」という考え方です。テクニカル分析の世界ではいろいろな数字が登場します。例えば、移動平均線では、5、10、20や6、13、26といった数字が出てきます。また、フィボナッチでは3、5、8、13、21といった数字とともに0.618という数字が出てきます。 そして、ここでご案内する一目均衡表には「基本数値」と呼ばれる数字があります。9・17・26の3つは単純基本数値と言います。9を2倍して1を引いたものが17、同様に9を3倍して2を引いて26になります。数字を引く理由としましては、例えば9日上げて9日下げた場合、最初の安値から高値を9日と数え、高値から最後の安値を9日と数えます。高値は同じ日を二度数えているため、重複した分1日を引きます。この単純基本数値に組み合わせる数値として33・42・52・65・76があり、これらは複合数値と言います。
相場における基本数値
9を一節、17を二節、26を三節としており、また、三節は一期とされています。 三期で一巡(=76)、三巡で一環(=226)、三環で一巡環(=676)です。
- 上昇相場:
最初の一波動を一節(9日)、中間の押し目と最後の一波動と大底からの一波動を二節(17日)を基本数値とされています。波動は長くても129日か172日で転換すると考えられています。 - 下落相場:
第一波動を33日とし、一節、二節は一時的な止まり値や中間の戻り値で出現することが多いとされています。
対等数値
また、基本数値ではないのですが、「対等数値」という考え方があります。過去の変化日と変化日に要した期間が次の変化日の目安になるというものです。この点を「日柄」と呼びます。
実は、私が投信会社でファンドマネージャーをしていた頃の上司だった部長が一目山人の弟子だったのです。「土曜日の午後に一目山人の家に集まり、勉強した」とよく聞かされました。その部長は「一目均衡表で大事なのは時間の考え方である」と言って、この対等数値の考え方を教えてくれました。この対等数値は前述した基本数値の数字にこだわる必要はありません。過去の変化日から要した日数を勘定すればいいのです。
波動論
一目均衡表の根本原理の一つである基本波動は3つあります。
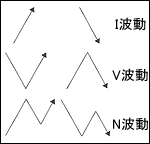
- 上げだけ、下げだけの「I波動」
- 上げ下げ、下げ上げの「V波動」
- 上げ下げ上げ、下げ上げ下げの「N波動」
I波動、V波動が繰り返され、最終的にはN波動になります。上昇し始めた価格は、N波動を完成するまでは下降に転じることはなく、下降し始めた価格はN波動を完成するまでは上昇に転じないという考え方です。
水準論
水準論は値幅観測論とも言われており、目標値を計算するときに使われます。
代表的なのは4種類です。
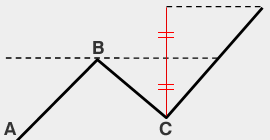
| V計算値 | B+(B-C)
|
|---|---|
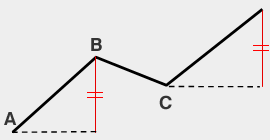
| N計算値 | C+(B-A)
|
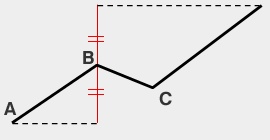
| E計算値 | B+(B-A)
|
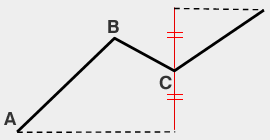
| NT計算値 | C+(C-A)
|
それでは、時間論と水準論(値幅観測論)を使って実際の銘柄を見てみましょう。
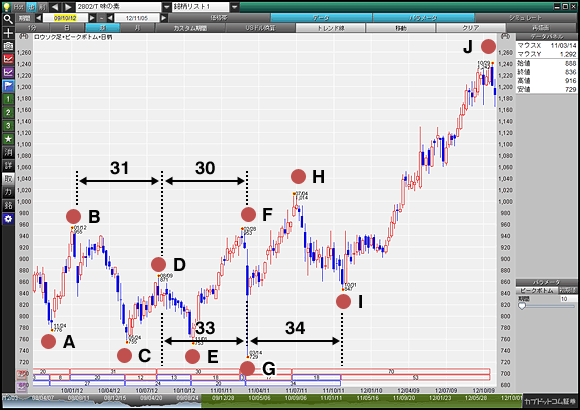
上図は味の素(2802)の2009年10月12日からの週足(約3年)です。
A:776円 B:955円 C:755円 D:871円 E:753円
F:953円 G:729円 H:1014円 I:847円 J:1242円
時間論の観点から、日柄にて対等数値をチェックしてみると、高値Bから高値D点までが31日、高値Dから高値Fまでが30日と対等。また高値Dから安値Gまでが33日、安値Gから安値Iまでが34日と、ほぼ対等となっていることがわかります。
次に水準論の観点から分析してみましょう。
E計算値
安値C:755円と安値D:871円のE計算値は987円になります。
871+(871円-755円)=987円
これは高値H:1014円とほぼ一致しています。
N計算値
安値A:776円と高値B:955と安値C:755円のN計算値は934円になります。
755+(955円-776円)=934円
これは高値F:953円とほぼ一致しています。
V計算値
高値D:871と安値E:753のV計算値は989になります。
これは高値H:1014円とほぼ一致しています。
871円+(871円-753円)=989円