第6回 ボリンジャーバンド
ボリンジャーバンドは移動平均線の上と下に線(バンド)を引くというものです。
その線の引き方に使われるのが、標準偏差という考え方です。
「標準偏差を用いる?」と首をかしげる方もいらっしゃるかもしれません。
標準偏差はデータがその平均値よりもどれぐらい散らばっているのか(離れているのか)ということを表したものです。
テストの点数を例にもう少しわかりやすく説明してみます。
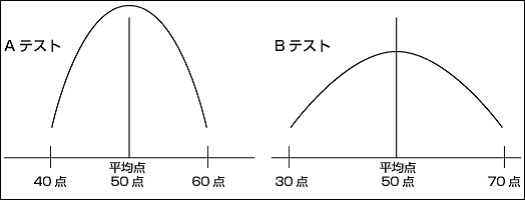
AテストもBテストも平均点は同じ50点です。
ただし、Aテストの方が平均点前後の点数を取る人が多かった。つまり、50点の平均点の近くの点数を取っていた。
これをマーケット的に見ると 移動平均の近くの値で推移している、つまり、安定的であるということです。
Bテストの方は、平均点は50点ですが、良くできた子供もいれば、点数の極端に悪かった子供もいるということです。
株価の動きで言うと、移動平均から大きく上や下に離れた価格もある。つまり、振幅激しく大きく動いているということになります。
このとき、平均点を中心に全体の約68%のデータが入る左右の点数、Aであれば40点と60点、つまり平均点からプラス・マイナス10点のところに68%のデータが入るということになります(あくまでも統計学上の話ですが)。
Bテストの方は平均点からプラス・マイナス20点の範囲に68%データが入るとされています。なぜならば、点数が散らばっているので68%のデータを入れるのにより平均点から離れなくてはならないからです。
この平均点から68%のデータが入る平均点からの距離を標準偏差(1標準偏差)と言います。Aテストの場合は1標準偏差10点、Bテストの場合は20点となるのです。
そして、平均点から2標準偏差、Aテストの場合は20点、Bテストの場合は40点離れた場合にはデータのおよそ95%がその中に入るとされています。
つまり、Aテストの場合30点から70点の間に受験した子供の95%の人数がいるとされるのです。
マーケット的に見ると、過去の任意の期間の値動きから標準偏差を計算するとその期間の移動平均からプラス・マイナス1標準偏差離れた範囲内に68%のデータが収まり、2標準偏差の間には95%のデータが収まることになるのです。
例えば、平均が100円で1標準偏差が10円であれば90円から110円の間に全データの68%の、この場合は過去の終値データが入っている、ということになっています。2標準偏差だと20円になりますから80円から120円までの間に95%のデータが入ってくるということになるのです。
となると、値動きが激しい場合には値段の散らばりが大きくなりますので、移動平均からからの距離、標準偏差は大きな数字になります。逆に、値動きが小さいと標準偏差は小さな数字になります。
こうした標準偏差と移動平均とを組み合わせたチャートがボリンジャーバンドなのです。
作成方法
移動平均線より例えば2標準偏差離れている場所に上下2本の線を引いていくというものです。
移動平均線+1標準偏差(ないしは2標準偏差)
移動平均線から一定率乖離させた線を引いていくエンベロープというテクニカル分析もあるのですが、乖離率だと相場があまり動いていない時でも、例えば5%であれば5%、大きく動いている時でも5%と常にどの状況でも同じ%で見ていかなくてはならないのですが、ボリンジャーバンドであれば余り動いていない時には変動幅が小さく、よって標準偏差も小さくなり、大きく動いた時にはその幅が大きくなっていくというものです。その都度その都度相場の局面における移動平均からの乖離度というものがわかるわけです。
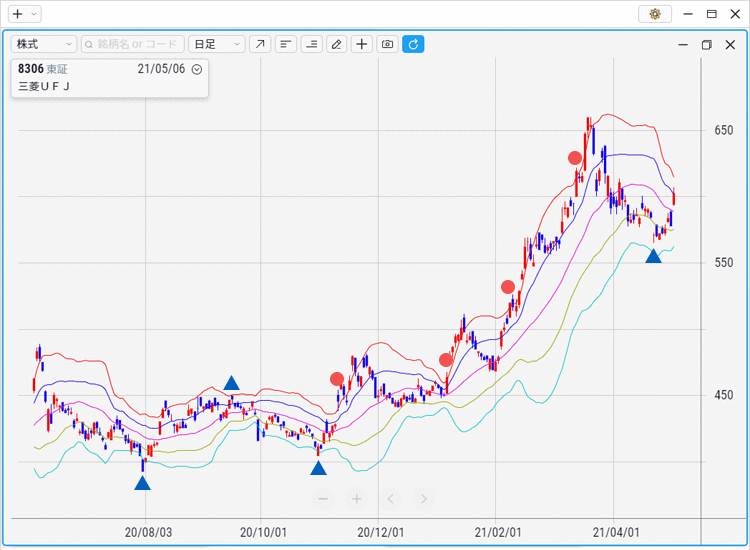
価格が保ち合いで横バイになっている箇所ではこの幅が縮小し、大きく動いている場面では幅が大きくなっています。
売買ポイント
2標準偏差というものはその中に約95%の確率で入ることを意味しますので、価格がその線に近づいた時にそろそろ逆の動きになるのかな、と考えます。
例えば、もし価格が上昇して上の線に近づいたのであれば“売り”を考えてもいいのかな、逆の場合には下の線に“買い”を考えてもいいのかな、ということになります(▲)。
また、保ち合いした後、幅が小さくなったところの2標準偏差をブレイクするような動きがあれば“新しい展開、局面”に入ったとしてそこを“買い”、“売り”とする場合もあります(●)。